Не развертывая определителей доказать следующие тождества.

АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ

Пусть имеем определитель третьего порядка: .

Минором , соответствующим данному элементу a ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i -ой строки и j -го столбца. Миноры соответствующие данному элементу a ij будем обозначать M ij .

Например , минором M 12 , соответствующим элементу a 12 , будет определитель 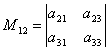, который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a 12 , берётся со знаком “–”, т.е. можно записать, что

(1)

Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.

Введём ещё одно понятие.

Алгебраическим дополнением элемента a ij определителя называется его минор M ij , умноженный на (–1) i+j .

Алгебраическое дополнение элемента a ij обозначается A ij .

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A ij = (–1) i+j M ij .

Например,

Пример. Дан определитель . Найти A 13 , A 21 , A 32 .

Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:

Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.

Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:

Разложим полученный определитель по элементам 1-ой строки.

(2)

Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a 21 , a 22 , a 23 . Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.

Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.

Таким образом, справедлива следующая теорема.

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

Всё вышесказанное справедливо и для определителей любого более высокого порядка.

Примеры.

ОБРАТНАЯ МАТРИЦА

Понятие обратной матрицы вводится только для квадратных матриц .

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A -1 и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел)

§ 4. Свойства определителей

Свойство 1. Величина определителя не изменится, если все его строки заменить столбцами, причём каждую строку заменить столбцом с тем же номером, т. е.

=
.

Свойство 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на - 1. Например,

= -
.

Свойство 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

Свойство 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k . Например,

= k
.

Свойство 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случай предыдущего (при k = 0).

Свойство 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

Свойство 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце, или соответственно в n-й строке, имеет первые из упомянутых cлагаемых, а другой - вторые; элементы, стоящие на остальных местах, у всех трёх определителей одни и те же. Например,

=
.+

Свойство 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,

=
.

Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путём вычёркивания строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число чётное, и с обратным знаком, если это число нечётное.

Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, которой обозначен сам элемент.

Свойство 9. Определитель

 =

равен сумме произведений элементов какого-либо столбца (или строки) на ихалгебраические дополнения.

Иначе говоря, имеют место следующие равенства:

 = a 1 A 1 + a 2 A 2 + a 3 A 3 ,  = a 1 A 1 + b 1 B 1 + c 1 C 1 ,

 = b 1 B 1 + b 2 B 2 + b 2 B 2 ,  = a 2 A 2 + b 2 B 2 + c 2 C 2 ,

 = c 1 C 1 + c 2 C 2 + c 3 C 3 ,  = a 3 A 3 + b 2 B 2 + c 3 C 3 .

В задачах 1217-1222 требуется, не раскрывая определителей, доказать справедливость равенств.

1217.
=
.

Указание, Воспользоваться свойством 8.

=
.

У к а з а н и е. Воспользоваться свойством 8.

1219.
=0

Указание. Воспользоваться свойствами 7, 3, 6.

1220 .
=0

У к а з а н и е. Воспользоваться свойствами 7 и 6.

1221.
=0 1222.
=0

В задачах 1223-1227 требуется вычислить определители, пользуясь одним свойством 9.

1223.
. 1224.
.

1225.
. 1226.
.

1227.
.

1228. Определители, данные в задачах 1223-1227, пользуясь свойством 8, преобразовать так, чтобы в каком-либо столбце (или строке) определителя два элемента стали равными нулю, а затем вычислить каждый из них, воспользовавшись свойством 9.

В задачах 1229-1232 требуется вычислить определители.

1229. . 1230.

1231.
.1232. .

1233. Доказать справедливость равенств:

1)
= (sin α - sin β) (sin β - sin γ)(sin γ - sin α);

2)
=

1234. Решить уравнения:

1)
= 0 2)
= 0

1235. Решить неравенства:

1)
< 1 2)
> 0

Определителем - го порядка, соответствующим квадратной матрице порядка , называется алгебраическая сумма членов, составленная следующим образом: членами суммы служат всевозможные произведения элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем член
берется со знаком плюс, если перестановка
содержит четное число инверсий, и со знаком минус- в противном случае. При этом инверсией чисел и называется ситуация, в которой
, но стоит в перестановке
раньше, чем . Для определителя матрицы
будем использовать обозначения или
.

Определители первого, второго и третьего порядков вычисляются по формулам, вытекающим непосредственно из определения:

При вычислении определителей третьего порядка удобно пользоваться “правилом треугольников”, отраженным по следующей схеме:

+ ¾

Из определения определителя следует, что:

Таким образом определитель диагональной, верхней и нижней треугольных матриц равен произведению диагональных элементов.

Основные свойства определителей :

Определитель не меняется при транспонировании.

. От перестановки двух строк (столбцов) определитель меняет знак.

. Определитель, содержащий две равные строки (столбца), равен нулю.

. Если все - строки (- го столбца) определителя представлены в виде суммы двух слагаемых, то и весь определитель представляется в виде суммы двух определителей, у которых все строки (столбцы), за исключением - й (- го), такие же, как в исходном определителе, а - я строка (- й столбец) в первом определителе состоит из первых слагаемых и во втором- из вторых. Например:

. Если все элементы некоторой строки (столбца) умножить на число, то определитель умножится на это число. Общий множитель элементов строки (столбца) определителя можно выносить за знак определителя. Если все элементы определителя умножить на число , то определитель умножится на .

. Если одна из строк (один из столбцов) определителя состоит из нулей, то определитель равен нулю.

. Определитель не меняется, если к элементам одной его строки (столбца) прибавить соответствующие элементы другой его строки (столбца), умноженные на одно и то же число.

Пример 1. Определите число инверсий в перестановке 2,3,8,1,4,5,7,6.

Решение . Поскольку 2 стоит в перестановке раньше, чем 1, 2 образует в перестановке одну инверсию. 3 также образует одну инверсию, 8- пять инверсий, т.к. стоит раньше, чем 1,4,5,7 и 6. Продолжая, получаем, что общее число инверсий в перестановке

Пример 2. Пользуясь только определением, вычислите определитель.

Решение . В соответствии с формальным определением определителя

Запишем все ненулевые произведения элементов матрицы и соответствующие им перестановки:

Учитывая, что

окончательно получаем:

Пример 3. Применяя свойства, вычислите определитель
.

Решение . Для вычисления определителя воспользуемся методом приведения его к верхнему треугольному виду. Метод заключается в преобразовании определителя к такому виду, где все элементы, расположенные ниже главной диагонали, равны нулю. Полученный определитель равен произведению элементов главной диагонали.

Переставим первую и четвертую строки определителя. Определитель изменит знак:

Первую строку последнего определителя, умноженную на , прибавим ко второй его строке; первую строку, умноженную на
, прибавим к третьей строке; первую строку, умноженную на
, прибавим к четвертой строке. Получим:

Переставим вторую и третью строки полученного определителя; вынесем общий множитель элементов второй строки за знак определителя. Получим:

Вторую строку определителя, умноженную на
, прибавим к третьей строке; вторую строку, умноженную на
, прибавим к четвертой строке. Имеем:

Переставим третью и четвертую строки. Третью строку полученного определителя, умноженную на , прибавим к четвертой строке. Приходим к определителю верхней треугольной матрицы